蕾樂斯和「惡魔」進入了矩陣的核心之中。他們展開了在數學上的運算戰爭,先從有限數開始。
他們先從0邁入了1的階梯。同時0和1也是組成二進制的唯二兩個數字。
戰爭開始。
先從如何構造一個大數開始。
3+3+3=9
3×3×3=27
3的3次方的3次方,用3^3^3來表示。
3的3次方是27。所以3^3^3=3的27次方。
但是這樣的增長速度實在太慢了。他們需要一個更快的運算方法,讓自己能夠在這場數學戰爭中取得勝利。
於是雙方都使用了高德納箭頭。


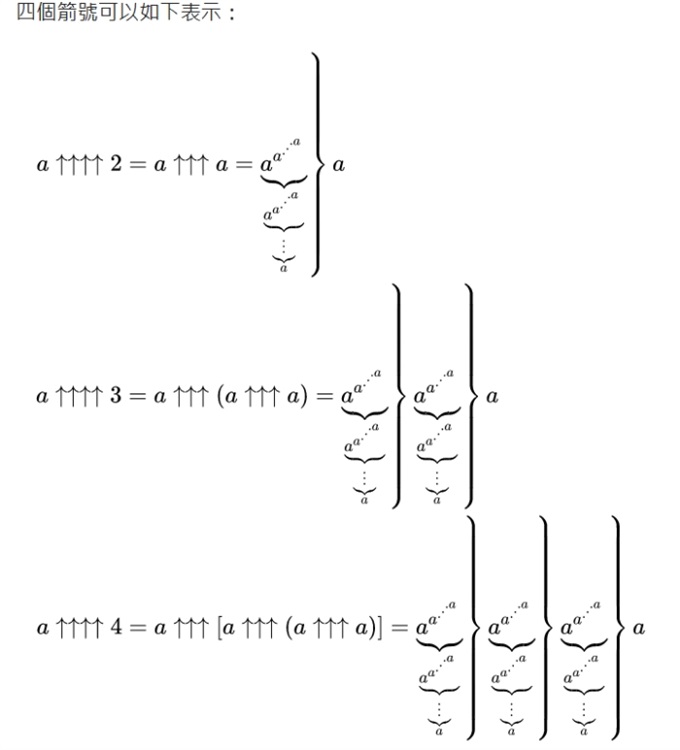
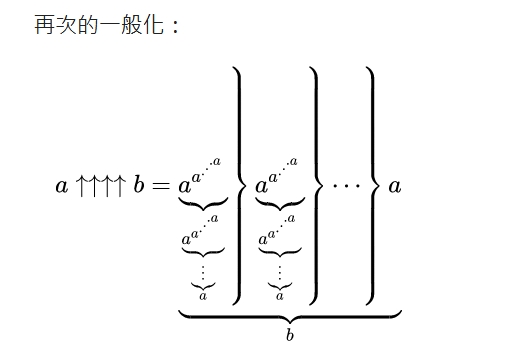
然後,他們到達了葛立恆數。
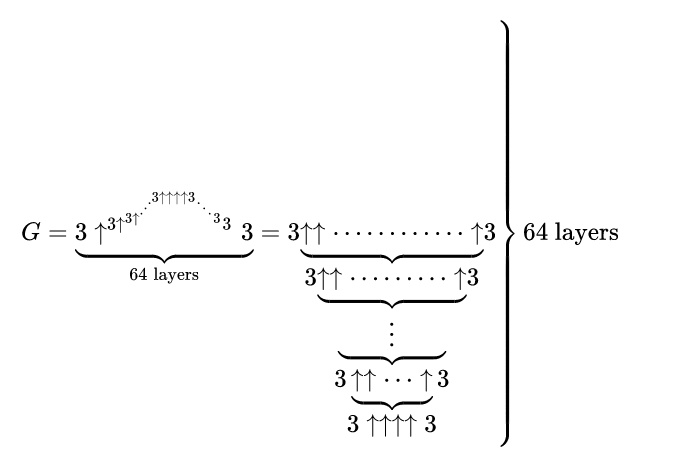
葛立恆數有多大?
我們可以大概的說一個比方。
宇宙直徑為920億光年=8×10^26米。
普朗克長度=1.6×10^-34米。
我們把宇宙當成一個正方形立方體,然後橫切、豎切它,把它切成一堆普朗克長度的正方形立方體,每一個普朗克長度寫一個數字,一共能寫10^183各數字。但相比葛立恆數,仍然是微不足道,相等於0,甚至比不過最底層的3↑↑↑↑3。
把葛立恆數裝到你的腦子內,會造成腦信息量太大,超過了黑洞的熵,把你的腦子變成一個黑洞。
但是這還不夠。
他們進入了超運算的領域。
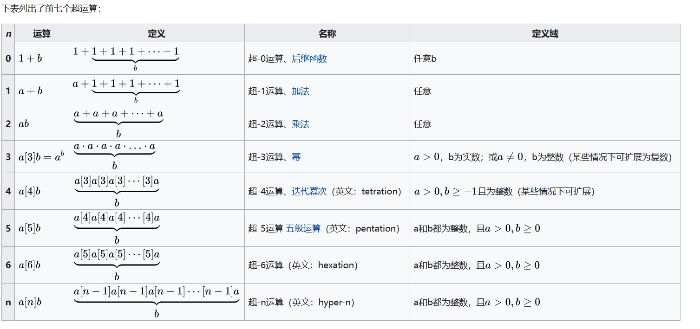
用比較易懂的方式解答。
a[1]b=a+b
a[2]b=a×b=a[1]a[1]a……[1]a(一共有b個a進行超-1運算)
a[3]b=a^b=a[2]a[2]a……[2]a(一共有b個a進行超-2運算)
a[4]b=a[3]a[3]a……[3]a(一共有b個a進行超-3運算)
以此類推……
不過,超運算要從後往前算。
例如2[4]4=2[3]2[3]2[3]2
=2[3]2[3]4(先把最後面的兩個2次方,得出4)
=2[3]16(把最後面兩個數字計算,就是2的4次方,等於16)
=2^16(2的16次方)
現在定義超N運算,就是a[n]b。
A是底數,B是超指數,N是階數。
這表示了有b個a進行超[n-1]階運算。
比如説2[5]4=2[4]2[4]2[4]2(一共4個2)
=2[4]2[4]4(2[4]2等於2^2=4)
=2[4]65536(然後2[4]4等於2^16=65536)
=2^2^2……^2(一共65536個2)
現在利用超運算定義一個阿克曼函數。
定義A(x)=2[x+1]x
A(1)=2[2]1=2
A(2)=2[3]2=2^2=4
A(3)=2[4]3=2^2^2=16
A(4)=2[5]4=2^2^2……^2(一共65536個2)
以此類推。
但是這個函數增長速度仍然不夠快。
如何纔能夠更快呢?
舉一個例子。
我打開一個空白word文檔。
如何纔能夠以最快的速度打字?
一個字一個字打增長率就是1,不夠快。
有一個辦法。
複製粘粘。
打了十個字,然後複製粘粘。增長率就是原來的十倍。
但依然不夠快。
複製粘粘十次後,一共有一百個字。然後把這一百個字全選,再複製粘粘。增長率達到一百倍了。
一千個字時再次全選複製粘粘。增長率達到一千倍。
不斷的重複,打字速度就會不停的增長。
這個辦法帶來的是函數的嵌套。
再次以阿克曼函數為例。
如何纔能夠使函數值超級大?
不是把A(x)當中x的數值變大。因為這太慢了。
你把x寫成一億兩億上去也不夠快。
現在已知A(4)的數值十分之大。
那就把A(4)放入函數之中。
形成A((A(4))。
把上一個函數的結果當成自變量輸入進去。
這就是函數的嵌套。
也可以再套一層,形成A(A(A(4)))。
但是如果想套一百層就需要寫一百個A,過於麻煩。
所以需要將其簡化。
把一百寫到函數中A的右上角。
也就是A^100(4),如此便是進行了一百次嵌套。
葛立恆數大約等於A^64(4)。
而超運算帶出了另一個比葛立恆數更大的數字,TREE(3)。
它的數量級是A(1)嵌套A函數A(187196)次。
A^A(187196)(1)
=A(A(A(A(A……(A(A(1)) )……)一共嵌套了A(18796)層。
比如說你寫個1,後面不停的寫0。從宇宙大爆炸開始,每一個普朗克時間寫一個0。普朗克時間是10^-44秒。這意味著每秒鐘你能寫10^44個0。
就算這樣從宇宙大爆炸一直寫到宇宙毀滅,你寫的數也沒有TREE(3)大,甚至約等於0。
一切的數學公式在TREE(3)面前都失去了意義。因為人類目前沒有一條數學公式能夠應付或者是應用如此龐大的數字。
但TREE(3)並不是最大的大數。在它的後面還有SSCG(3)。
在數學中,簡單子三次圖( SSCG ) 是一個有限簡單圖,其中每個頂點的度數最多為 3。假設我們有一系列簡單的子三次圖G 1 , G 2 , ... 這樣每個圖G i最多有i + k個頂點(對於某個整數k)並且對於沒有i < j是G i 同胚可嵌入到 ( ie 是) G j的小圖.
Robertson-Seymour 定理證明了子三次圖(簡單或不簡單)是由同胚可嵌入性充分建立的,這意味著這樣的序列不可能是無限的。因此,對於k的每個值,都有一個具有最大長度的序列。函數 SSCG( k ) [1]表示簡單子三次圖的長度。函數 SCG( k ) [2]表示(一般)次立方圖的長度。
SCG序列從 SCG(0) = 6 開始,但隨後在快速增長的層次結構中爆炸到等於 f ε 2 *2的值。
SSCG序列開始SSCG (0) = 2, SSCG(1) = 5,但隨後迅速增長。SSCG(2) = 3 × 2 (3 × 2^95 ) − 8 ≈ 3.241704 × 10 35775080127201286522908640066及其十進制擴展以 ...11352349133049430008 結尾。
SSCG(3) 遠大於TREE(3)和 TREE^TREE(3) (3)。
Adam P. Goucher 聲稱 SSCG 和 SCG 的漸近增長率之間沒有質的差異。他寫道:“很明顯,SCG( n ) ≥ SSCG( n ),但我也可以證明 SSCG(4 n + 3) ≥ SCG( n )。”
Rayo數
Rayo 數的定義是:
比任何有限數都大的最小數,該數由一階集合論語言中的表達式命名且帶有googol符號或更少。
Rayo(10^100)BC
具體來說,該定義的初始版本(後來被澄清)為“大於任何數字的最小數字,該數字可以通過一階集合論語言中的表達式命名且小於 googol (10^100 ) 符號。
數字的正式定義使用以下二階公式,其中 [φ] 是哥德爾編碼公式,s 是變量賦值:
對於所有 R {
{對於任何(編碼)公式 [ψ] 和任何變量賦值 t
(R([ψ],t) ↔
(([ψ] = "x i ∈ x j " ∧ t(x i ) ∈ t (x j )) ∨
([ψ] = "x i = x j " ∧ t(x i ) = t(x j )) ∨
([ψ] = "(∼θ)" ∧ ∼R([θ] ,t)) ∨
([ψ] = "(θ∧ξ)" ∧ R([θ],t) ∧ R([ξ],t)) ∨
([ψ] = "∃x i (θ)"並且,對於某些 t 的 x i -變體 t',R([θ],t'))
)} →
R([φ],s)}
給定這個公式,Rayo 的數被定義為:
比所有有限數 m 大的最小數,具有以下性質:在一階集合論的語言中存在一個公式 φ(x 1 )(如Sat的定義中所示),其符號小於一個 googol 和 x 1作為其唯一的自由變量,這樣: (a) 有一個變量賦值 s 將 m 分配給 x 1使得 Sat([φ(x 1 )],s),並且 (b) 對於任何變量賦值 t,如果 Sat ([φ(x 1 )],t),然後 t 將 m 分配給 x 1。














