首先有生灵。
生灵的特性是进化,任何一个生灵都有超出自身,抵达更高阶段的潜能,我们将生灵的原始基准设置为1,低于这一基准值的不再被称为“生灵”。高于基准的下一个阶段称为S(1),记为2,注意到对于任意生命层次n,S(n)标记了它的下一个层次。
一般地,有两种生灵的类型。
第一种,称为“进化者”,此类生灵的特性是进化进程独立于生命层次,进化速度并不直接受到生命层次的影响,而是仅仅构成关于时间的函数。这使得无论进化者的进化函数有多高的增长率,总是存在进化速度更快的进化者,每个进化者都将在极其有限的时间内被拥有更高进化率的进化者超越,并在此后的所有时间里低于这些超越者,直到自身的进化速度发生变化。这种情况称为“进化支配链条”
进化者之间的强弱不仅仅取决于它们的当且生命层次,更取决于它们的进化速度,不仅仅取决于它们的进化速度,更取决于它们“进化速度的变化速度”,最广义而言,进化者的强度涉及它们的“深度”,与在不同“深度”上的增长率。最弱小的进化者的深度为0——仅仅具有最表层的生命层次,其余的层次要么不存在,要么值为0。即使进化者的进化速度构成关于时间的底数大于e的指数函数(其生命层次的变化速度将随着时间进展而越来越快),它依然只能在极其有限的时间内达到极其有限的生命层次。
第二种称为“升变者”,当生灵的生命层次直接对其进化速度造成影响,并且存在极其有限的时间内可以触碰的“奇点”时,该生灵被称为升变者。
一个简单的例子,某个生灵的进化模式如下:初始进化的时间间隔为t,生命层次为1,每提高一个生命层次都会导致进化间隔缩短一半,即在生命层次n时,下一次进化发生在t/2^(n-1)后,求和得到:2t(1-(1/2)^n),收敛于2t,在时间达到2t前,此生灵将会进行趋于无穷次进化,使得它的生命层次超越每一个可能的进化者——无论后者的进化速度有多高。
显然,任意一个升变者,无论它的奇点出现在何处,它都绝对地支配了任意一个进化者。
基于升变者拥有的这种超越支配链的特性,我们可以正式为前文中多次出现的“极其有限”一词做出如下定义:
称一个进化阶段n是极其有限的,当且仅当(def)任意升变者将在到达奇点前经历它
虽然此定义依然有非直谓的嫌疑,但这种定义的循环性仅仅是语义上的,升变者们的实在本身反过来为这一自引用的定义提供了“终结点”
一般认为,升变者通过加速进化到达的生命阶段可以被一种包含“无穷大数”的数系来建模,需要注意的是,升变者并不是在奇点处“停止了进化”,母宁说,它们将原本平铺在无限时间中的进化的无穷进展压缩到一个刹那,这个刹那将在其“无穷加速”中容纳进化的无限进程,以一种既非完成也非未完成的形式使得无穷远处的彼岸“在场”。而升变者的序关系也不再能够用“进化阶段”来表示——它们的每一个都已经跨过了任意一个进化阶段——而应该引入新的指标,不妨称之为“奇点指数”
我们可以进一步得到以下两个原则:
1.不存在最弱或最强的升变者
2.对于任意升变者,存在着任意多与它“足够接近”的升变者,这里的“足够接近”指当到达奇点后,它们之间的奇点指数仅仅相差一个极其有限的值。
我们将t*=t/2^(n-1)序列的升变者的奇点指数记为N,注意到,N其实就是以上无限序列的倒数简化掉时间参数(时间对于升变者来说并无意义)后得到的另一个无穷序列:
N=(1,2,4,8...)
而奇点指数为N+1的升变者则具有以下序列:
N+1=(2,3,5,9...)=(1,3,5,9...)=...
值得注意的是,虽然N与N+1之间仅仅差了一个极其有限的值——1,但N+1代表的序列依旧在“几乎每一位”上都大于N,这种关系类似于进化者之间的“支配”关系。我们在这里发现一个有趣的现象:对于非生灵而言,衡量差距的最有效标准是“阶段”本身的高低,而到了进化者之中,“阶段”本身的高低只是一个暂时的,且终将被颠覆的标度,衡量进化者之间差距的有效标准是其在“支配链”上的高低,但到了升变者这里,这种“类支配关系”本身也变得微不足道——任意两个奇点指数间仅仅相差极其有限值的升变者都是“足够接近”的,我们可以用如下图示来代表升变阶段与进化阶段的根本性差异:
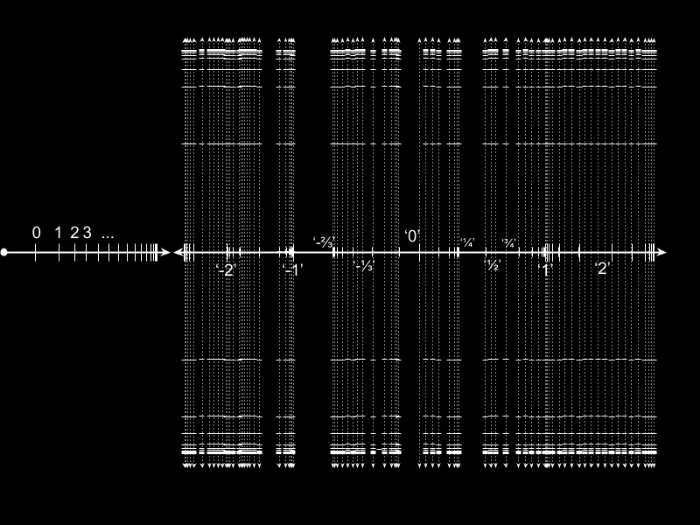
可数非标准自然数系的序型是ω+(ω+ω*)η
其中ω是标准自然数集的自然序型,ω*是无穷降链的序型,η是有理数集的序型
ω+(ω+ω*)η这一序型表示的含义是,在标准自然数集(进化者阶段)之后,存在着非标准自然数(升变者阶段),每一个非标准自然数(广义升变者)都是一个序型为(ω+ω*)的“块”,代表了其向着两个方向的无限扩展,而η是稠密线性序的序型,代表这些非标准自然数的“块”绝对稠密地排列着。
“每一个升变者都是一个无穷实体”,这不仅仅是在说跨过奇点的升变者在“进化阶段”上高于任意多个可能存在的进化者,并且,就升变者的体系-构成-本体而言,每一个升变者都内在地是一个进化者的无穷序列,这些进化者拥有任意高的初始生命层次与相同的进化速率——这一速率实际上由升变者本身通过生命层次对自身进化速率造成的影响程度决定。
设一个升变者奇点前的进化阶段为E,“进化阶段”提升的速率为f(E),且E与t之间存在影响,在这里将E视为关于t的函数,得到微分方程:
dE/dt=f(E),解得E=∫ 1/f(E) dt
当f(E)满足一定条件,例如f(E)是以E为底指数大于1的幂函数时,E将在有限的时间内趋于无穷大
依然以t/2^(n-1)消t反序列对应的升变者为例,N=(1,2,4,...,2^n-1,...),其中每一个升变者的进化函数都为以t为自变量,增长率等价于2^n-1的单调数论函数。
而一个严格强于N的升变者可以是N+N,
N+N=(1x1,2x2,4x4,...,2^n),注意到N+N展开的序列中,不仅“几乎每个”进化者都强于N序列中的对应进化者,并且几乎每个进化者都支配了N序列中的对应进化者。从更直观的奇点指数上看,N+N不仅大于N,而且“无限地”大于N
同样地,在无限地强于N的升变者中,依然不存在最弱的一个——N+N/2,N+N/4...
有了从N到N+N的进程,自然也能将其推广到更高的层次上,例如NxN=(1²,2²,4²...),N^N=(1^1,2^2,4^4...),N^^N=(1,2^^2,4^^4...),乃至于任意超-数论函数f,
f(N)=(1,f(2),f(4)...)
在对超数论函数进行考察时,我们发现了一个有趣的现象——如果我们用超自然数N代替极限序数ω作为函数在快增长层次中的指标,那么f_N(x)和f_ω(x)在标准数上的表现是一致的,同理,f_N^N(x)和f_ω^ω(x)具有相同的数论表现,如此这般,我们可以重新定义以超自然数为下标的fgh超-数论函数在非标准自然数上的作用机制,如:
f_N(N)=(1,f_N(2),f_N(4)...)
以下是一个粗略的对照表:
N~ω
N+n~ω+n
Nxn~ωxn
N^n~ω^n
N^^N~ε0
(N^^N)^ N~ε0^ω
N^^N+1~ε0^ε0
N^^Nx2~ε1
N^^Nxn+1~εn
N^^NxN~εω
N^^(NxN+NxN)~εωx2
N^^(NxNxN)~εωxω
N^^(NxNxN+NxN)~εωxω+ωx2
N^^(NxNxNxN)~εωxωxω
N^^(N^N)~εω^ω
N^^(N^N^N)~εω^ω^ω
N^^(N^^N)~εε0
N^^N^^N^^N~εεε0
N^^^N~φ(2,0)
N^^(N^^^N)~φ(1,φ(2,0))
N^^^(N+N)~φ(2,1)
N^^^N^^^N~φ(2,φ(2,0))
N^^^^N~φ(3,0)
f_N(N)~φ(ω,0)
f_f_N(N)~φ(φ(ω,0),0)
f_f_f_f...(N)~φ(1,0,0)
...
f_(1,0,0,N)(N)~φ(1,0,0,0)
f_(1(N),N)(N)~φ(1@ω,0)
f_(1[1],N)(N)~LVO
...
理论上来说,任意一个可以被写出的序数,都存在一个对应的N-形式
正如不存在一个支配了一切进化者的进化者一般,不存在一个在其内生序列中“二阶支配”了一切升变者的升变者,而在不违反这一条基本原则的情况下,如何得到更进一步的,甚至超越升变者的推广呢?我们可以考虑仿造在自然数系N上构建可数超自然数系N*的方法,即首先取N为基结构,ω为指标集,ω上超滤为核心的超幂模型,然后通过向下司寇伦定理与Mostowski坍缩得到超幂模型UltuN的可数传递子结构,记为(N**,∈)
可以称为超*自然数结构
同样的,每一个超*自然数都是超自然数组成的无穷序列,称一个超*自然数大于另一个,是在说在序列的“几乎每处”,都有对应的超自然数大于另一方,例如
N*=(N,N,N...),其大于任意标准自然数与非超*自然数的超自然数
N*+1=(N+1,N+1,N+1...)与N*足够接近
而N*+N=(N+1,N+2,N+4...)也与N*足够接近
只有当超*自然数内生序列中的每一项都与另一个序列内的每一项拉开至少一个超自然数的差距时,才有Q*在超*自然数的序上“大于”另一个P*
不妨将由超*-自然数建模的超-无穷实体称为三阶生灵,它们之间的序关系需要以“三阶支配”来描述
同样的,这样的操作可以一直向后推广,四阶生灵的模型是超**自然数的模型,其搭载的序关系是四阶支配,接下来,五阶六阶乃至更多,由于这个推广实际上是超幂迭代,因此可以在极限步取直接极限(direct limit),得到的极限实体(的可数传递子结构)可以被称为N-超自然数或ω-超自然数,继续推广也是十分自然的——最终我们得到了这样一幅图景:在一阶生灵为有限者的情况下,二阶生灵与一阶生灵之间有名为“无限”的隔断,而三阶生灵与二阶生灵之间“相隔”的不仅是无穷,更是绝对无穷(考虑到任意可以用序数记号在公理系统内固定的序数都有对应的N形式)的,而二阶之后,每一阶生灵间都因类超自然数的绝对可延展性而“相隔了越来越大的绝对无穷”,然后我们会看到,描述了上升的生灵阶次的指数本身更是“超越此前一切绝对无穷的绝对-绝对无穷”,甚至于,即使是这个阶次系统本身亦能够被进一步推广,从而滋生出更多不可名状的绝对-绝对-绝对无穷,绝对-ω-无穷,绝对-(绝对-(绝对...))-无穷
这一切不过是对早已发生在升变者阶段的事件的重演
然后,我们回到一开始的中断点——没有任何进化者拥有超越一切进化者的进化函数,当我们能够谈论“一切”的时候,必定有一个超越了此等“一切”的外生性实体给予了我们“一切”的谓词,例如升变者反规定了一切“极其有限”,三阶生灵反规定了一切“无限”,四阶生灵反规定了一切“超无限”等等,而那个规定了“一切”的一切,一切的一切的一切,以至于让“一切”本身都湮灭在纯然无法言说的绝对深渊里的“非-者”,暗示性地成为了诸如“支配一切进化者的进化者”,“集所有内生增长模式于一身的升变者”,“超越一切n阶生灵的n阶生灵”的悖论性实体,就是那无需逻辑也从未被指涉的“真绝对无穷”














