我们刚刚说到要探究直角三角形的特点。
首先,先让我给你一个直角三角形,仍然使用上一章的图:
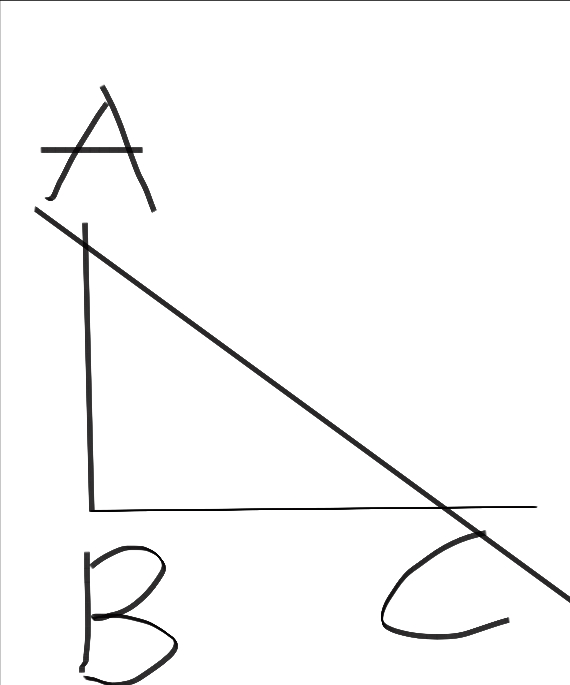
它有什么特点呢?
好吧,没有人能直接看出来它的特点。所以,我们不妨把它放进一个正方形里,也许这样能让你比较好的看出它的特点。
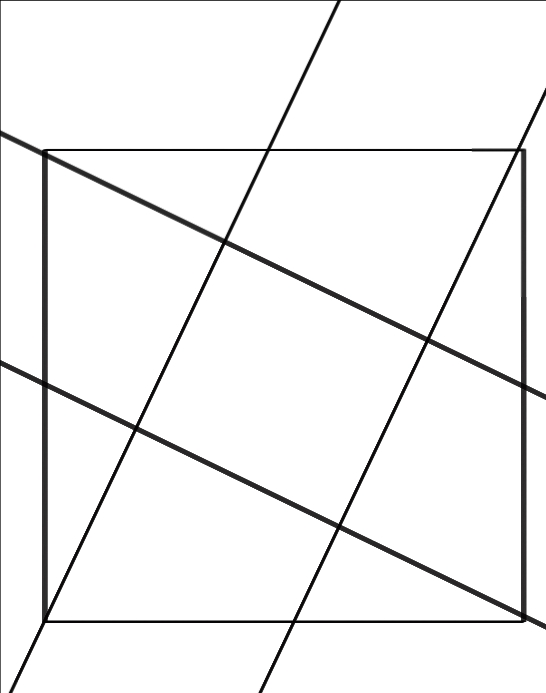
接下来我们稍微给他补充一下信息。
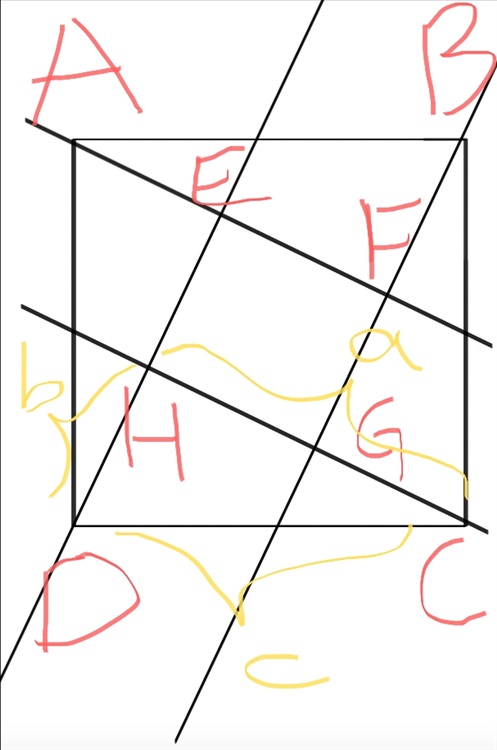
我设外边的大正方形为正方形ABCD,同时我过每个顶点作一条直线交正方形的其中一边的中点。
至于中间的图形,我可以先称呼他为四边形EFGH,毕竟我们现在还不知道它是什么图形,不过就肉眼可见,他显然是一个四边形。
说实话,我非常愿意带你继续深入研究,但我想带你见识一下另一个重要的东西。
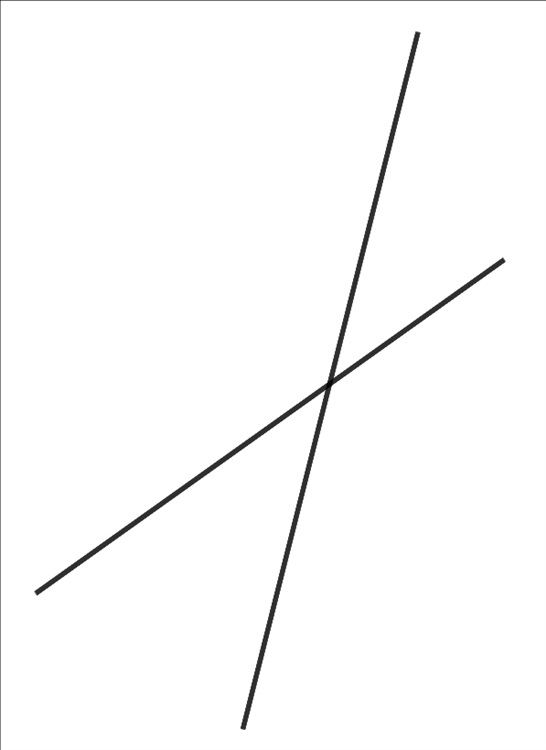
这是我们之前所用过的一幅图,我用它来向你解释了一些与直角相关的知识。
只是现在我要加一条直线。
如图:
现在这里有三条直线了。
肉眼可见他们一定是有交点的,所以我们可以称呼这种关系叫做相交。至于之前所说的垂直,那就是相交的一种特例。事实上,还有一种比较特殊的,那就是重合。但那又有什么意义呢?他俩是完全相等的!这样的话,我们还研究他们干嘛呢?所以一般情况下,只要我们不特殊强调重合,我们就默认两条直线不是重合的。
那么,你应该能想到,应该存在一种情况,使得两条直线无法相交。
他看上去应该像下图:

事实上的确存在这种情况,我们将它称呼为平行。
所以,两条直线间的关系简单来说有两种,一种是相交,一种是平行。而重合与垂直都是相交的特殊例子。当然,也仅限于现在。事实上,在空间中,直线的关系不仅是这两种。等到以后我们会了解到他的。
我需要说明的是,我所说的分类并不一定是被全部人认可的。我认为直线与直线要么相交,要么不相交,就这两种情况,所以分为相交和平行,并由此认为,重合是完全相交。但有的人认为重合太过于特殊,理应把它单独分类,不过这种情况应该不多。
无论如何,只要你明白了,直线与直线间有怎样的关系,以及为什么会有这样的关系就可以了。至于分类的事,就等到历史来盖棺定论吧。
接下来问题又来了。
平行意味着两条直线没有交点,这也是非常符合常理的。那么,怎样才可以证明两直线是否平行呢?
我们可以用尺子比划一下,让你把尺子的一边对准该直线,然后在保证不发生任何旋转的情况下平移至另一条直线,若该尺子边仍然能与新直线保持重合,那么我们就可以说这两条直线平行。
那么为什么这样做就可以了呢?
这很简单。
还记得我之前向你说过的角的相关知识吗?
我们可以认为:角能用来表示一条直线相对于另一条直线旋转多少。当然,我们现在知道了,严格来说是旋转多少度。因为角的单位就是度。那么,如果你能保证尺子不旋转而只是平移的话,那么我们就可以说这两条直线与尺子之间是完全重合的,也就是说相对于尺子边,这两条直线都未发生任何偏转。也就是说他们的方向与该尺子边是一致的。所以这两直线的方向也一定是一致的。
而如果他们想要有交点,你可以想象成是一条直线方向不变,而另一直线必须要有一个偏向该直线的方向,否则延长该直线则不可能向原直线的位置靠近。只有在延长时,他们有靠近的一种趋势,那么我们才能肯定的,说他们在之后的延长时一定会相交,无论这个交点看起来是多么的遥远。
而现在他们的方向一致,那么就与之前的结论相反,也就是说,他们不可能有交点。那既然都不可能有交点了,那他们的关系肯定就是平行了。
所以,根据这个思路,我们就有了如何判断两条直线是否平行的方法。
请看下图:

这有两条横着的直线,还有一条竖着的穿过这两直线的直线。
如果这两条横着的直线与竖着的直线的夹角相同的话,就像我们刚才说的那样,这两条横着的直线相对于这条竖的直线有着相同的夹角,那么这两条横着的直线的方向相同。
如果方向相同的话,那么他们就不会有交点,不会有交点,那么这两条直线自然就是平行的了。
当然,由于两两直线相交出现四个角,所以我们一般默认最小的那个角为两直线的夹角。当然,夹角夹角,夹着的角,所以那个大的显然也是个夹角,不过谁让我们更喜欢处理更小的东西呢?而且,角作为一个衡量两直线间具体的关系时,无论用小的角,还是用大的角,你一定会得出同样的结论。
就相当于你在操场上绕圈,你正着绕1/4圈,和反着绕3/4圈,最终到达的终点都一样。所以人们更习惯于用小的那个角来表示夹角。
所以在任何情况下,你都应当将较小的那个角作为两直线的夹角。
除非垂直,你才可以用较大的那个。但事实上,在垂直时,显然这两个角是相等的,他们没有大小之分。他们都是最大的角,但同时他们也是最小的角。
事实上,在我们刚才用尺子这一方法来判断两直线是否平行时,就算是这种方式的一个特例。毕竟,就以我们刚刚的操作来说,实际上是证明了这两条直线与尺子的夹角都为零度。
无论是零度也好,其他的度数也好,只要这俩度数相等,那么就一定有这两直线平行。
所以我们有如下结论:如果两条直线分别与另外一直线形成两夹角,而且这两个夹角的大小是相等的,那么我们就可以说这两直线平行。
反过来也成立。
如果有两直线平行的话,并且还有一另外的直线,那么这条另外的直线与这两条平行的直线所分别形成的两个夹角一定是相等的。
接下来我们将继续平行及相关证明,这是我们研究直角三角形,甚至是三角形之前的重要的知识。














