我们刚刚说完了平行的概念以及如何证明两条直线平行。
接下来我们需要学习一些其他的证平行的方法。我们仍然看这幅图:
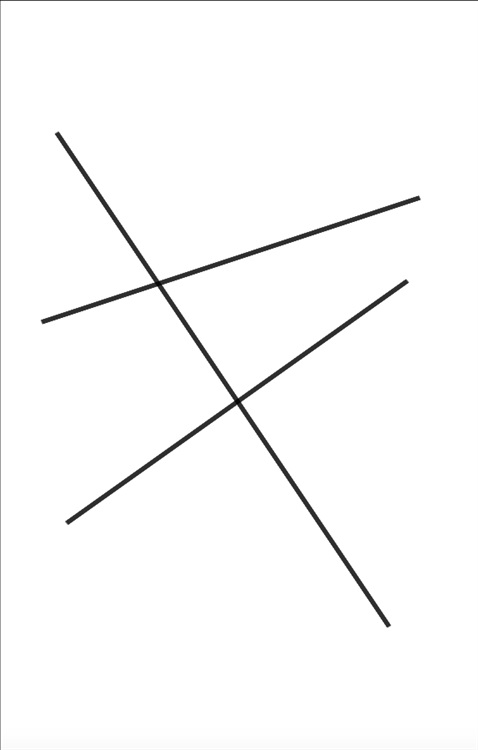
我们之前提到夹角,并且说明了为什么一般我们都要选择小的角作为夹角。所以在上一章,我们都是用夹角这个词来解释的。但这样还是不太严谨,对吧?让我们对这些角进行命名,以便我们更方便地来进行讲解。
如图:
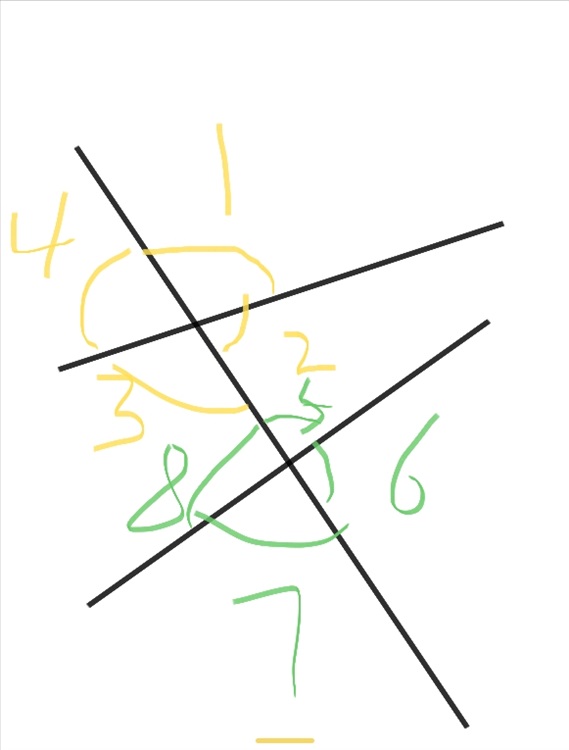
为了让你们看的更清楚,我将上面的四个角用黄色标记,而下面的四个角用绿色标记,并且画了一段小弧线用来表示这个角的大小,以及数字来对其进行标号。
现在我们可以用角1或者是角2这种具体的描述来说明问题了。
顺带一提,在数学上我们可以使用“∠1”来表示“角1”。其他的同理。当然,你也可以用一些希腊字母,比如,你可以用α,β,θ等希腊字母代替数字1。你也可以用字母来表示,如下图。
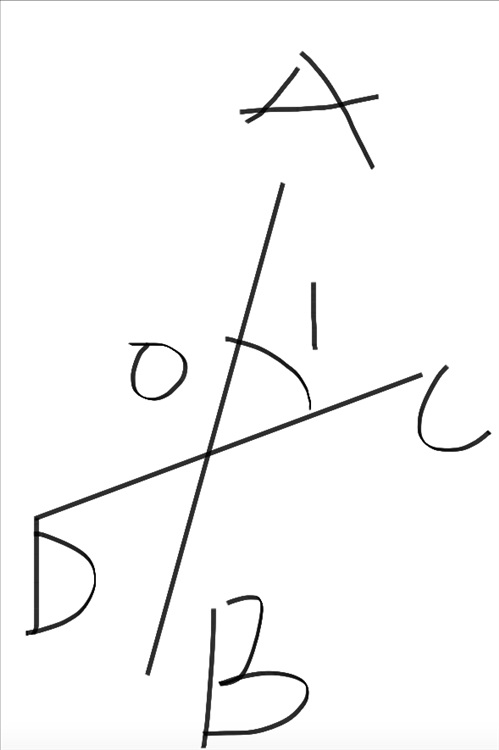
在该图中,有直线AB与直线CD相交,角1是我们要表示的角。由于两条直线的交点为O,所以角1可以表示为角AOC,用符号表示的话可以写成“∠AOC”。
说到这里,我向你补充一下角的相关知识。一个角申两条端点相同的射线组成,这两条射线分别称为角的两个边,而重合的端点被称为角的顶点。
非常简单,对吧?毕竟我们之前讲什么可都是要好几大段的。
顺带提一句,如果你因为这个定义,认为两直线构不成角的话,那你可以这样想,直线是向左右两端无限延伸的,而射线是向一端无限延伸的,所以直线可以看成是两个端点相同方向相反的射线。这不就符合角的定义了吗?
当然,无论怎么讲,直线绝对不可能等于两条射线的。但无论怎么讲,他们看上去真的没有什么不同。除非你在纸上画的时候把射线的端点画的太大了。
接下来我们仍然来看看这幅图。
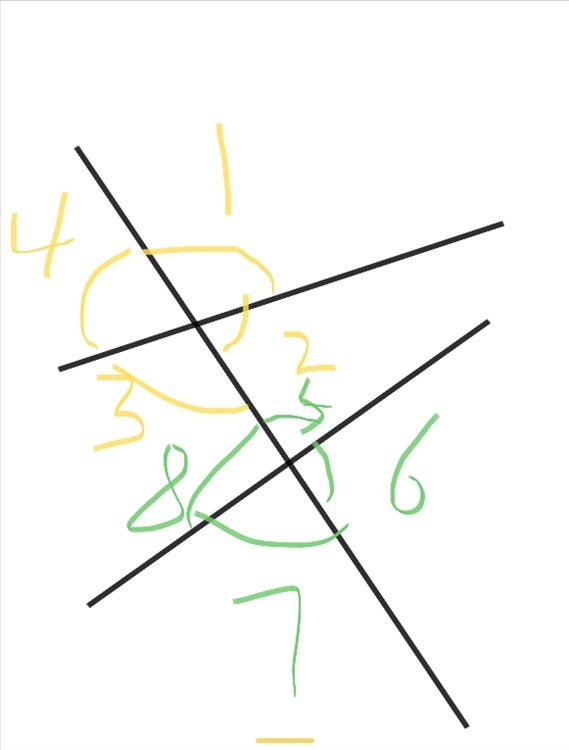
根据我们之前提到过的证明两直线平行的方法,如果在这幅图中,有角一等于角五,我们就能证明这两直线平行了。当然,角二等于角六,角三等于角七,角四等于角八都可以证明两直线平行。
所以,这些条件也都可以证明两直线平行。
但为了方便描述,我们把角一和角五,角二和角六,角三和角七,角四和角八称为一对同位角。
比如,角一和角五都在这两条要证平行的直线的上面,并且在另一条直线的右边,所以他们相对于这两条直线来说,具有相似的位置关系,所以我们就说他们是一对同位角,具有相似的位置关系的角。
所以,我们可以把上面一大段简化成如下一句话:若两条直线与另一直线相交,同位角相等,两直线平行。
接下来,我们继续来看这幅图:
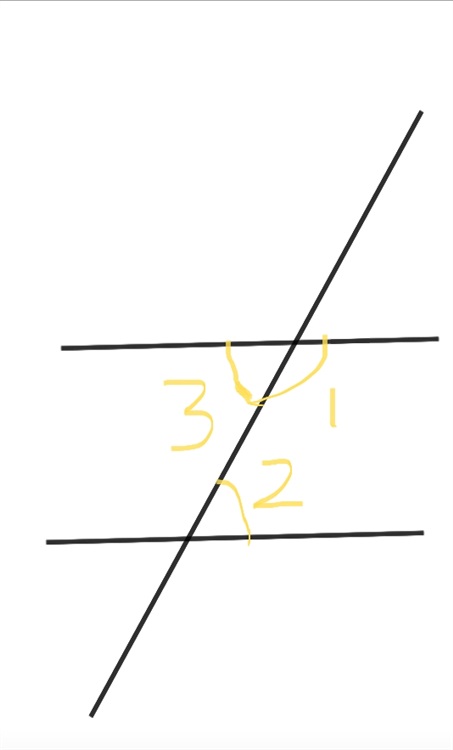
在这幅图中,如果有同位角相等的话,你还能得到什么?
你可以注意一下角一和角二。
事实上,这两角之和为180度。
因为角二与他的同位角相等,而角二的同位角与角一只和一定为180度,你可以看到这两个角有一边是重合的,另外两边都在同一条直线上,所以他们两角之和相当于一条射线旋转到该射线的反向延长线上,那么一定就是转半圈了,也就是180度。
顺带一提,这种180度的角叫做平角。
所以我们就可以知道。角一与角二的和,就等于角一与角二的同位角的和也就等于这个180度的大角,也就是说,角一与角二的和等于180度。
还有个知识,如果两角之和等于180度,我们就说这两个角互补。如果两角之和等于90度,我们就说这两个角互余。
这两个角由于都在这两条直线的内部,并且还在另一条穿过这两条直线的直线的同一侧,所以称呼他为一对同旁内角。
角一与角三之和显然也为180度,所以角二一定就等于角三,因为角一不可能加上两个不相同的数,还得到一个相同的的结果。由于角二和角三都在这两条直线的内侧,但却不在穿过这两直线的直线的同一侧,他们是错开的,所以我们称呼他为一对内错角。
让我们来梳理一下我们的思路。
如果有同位角相等的话,我们就能证明出来同旁内角互补和内错角相等。(严谨来讲,也许你要说明是一对同旁内角,以及一对同位角,毕竟没有“一对”这两个字的话,他看上去真的很像一个角。但谁让人们都喜欢这种简化的形式呢?放心大胆的去省略吧!)
反过来,如果有同旁内角互补,或者是内错角相等的话那么我们也能证出同位角相等,就是把刚才的过程反过来而已。
事实上,只要你得到这三个条件中的其中一个,你都能推出另外两个条件。而我们知道的就是,如果你得到的这三个条件,那么你就一定得到的同位角相等,那么你也就得到了两直线平行。
所以,只要你能得出这三个条件中的任意一个,你最终一定能挣出这两直线平行。
那反过来呢?如果你有两直线平行的话,那么你一定能得到同位角相等,那么你也就自然能得到,另外两个条件。所以,只要有两只线平行,你就有同位角相等,同旁内角互补和内错角相等。
总结:
同位角相等,两直线平行。
同旁内角互补,两直线平行。
内错角相等,两直线平行。
反之亦成。
两直线平行,同位角相等。
两直线平行,同旁内角互补。
两直线平行,内错角相等。
很好,由此我们算是彻底的搞清楚了,直线平行有怎样的特点,以及怎样的条件才能证明两直线平行。
不要小看他,我们马上就要利用它完美的解决一个看起来比较困难的问题。
在下一章,我们将使用我们刚刚学习到的平行的相关知识,去证明三角形的内角和为180度。
(本来以为这章能开勾股定理的,现在来看,至少这章是不可能了,我们尽力快一点)














