就让我们用刚刚学会的平行的相关知识,来解决三角形内角和为定值的这一问题吧。
首先让我们随意的画一个三角形,比如你可以画成下面这样。

但如果要证明内角和为180度的话,我们需要做一些能够帮助你完成你的目的的东西,比如,看看下面这幅图,这就是对上面的东西进行处理后的样子。
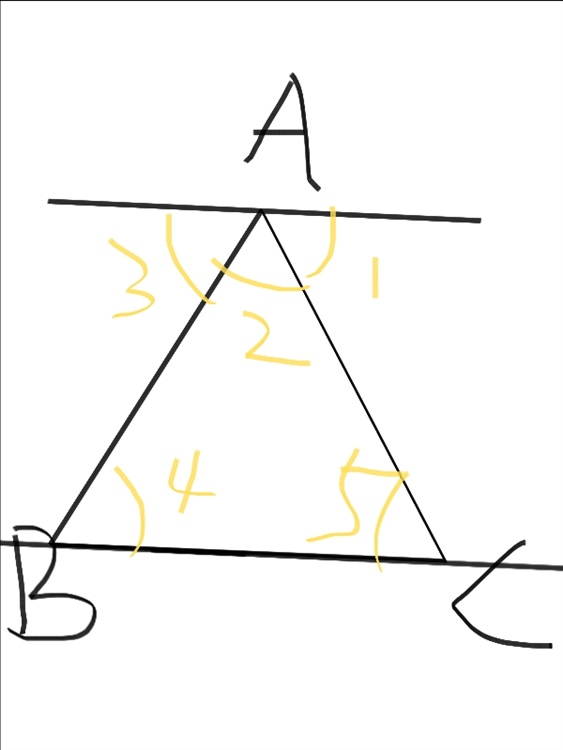
我们在线段BC的左右两端延长,做出直线BC,并将该直线向上平移致过点A处,这就意味着这两条是直线是平行的,因为你仅仅只是平移,而并未改变它的方向。
同时为了方便,我们对一些角标上了角一角二等符号,来帮助我们在证明的时候使得语言更加精练。
根据我们之前学过的平行关知识,你应该很轻易的看出角一等于角五,角三等于角四。因为两直线平行,内错角相等。
也就是说三角形的三个内角之和,也就是角二加上角四加上角五,可以被替换为角二加上角三加上角一。
但是角一加上角二加上角三刚好组成了一个平角,也就是一个180度的角,所以三角形的三个内角之和就等于180度。
到这里,我们就成功的证明了三角形的内角和为180度。但是严谨的来说,你只是证明了这一个三角形为180度,这世界上有那么多的三角形,你能证明他们都是180度吗?你现在还没有证明其他的三角形也都是180度,所以目前你还并不能说三角形的内角和一定为180度。
我不建议你一个一个的把遇见的所有的三角形全部证明一遍,那样太麻烦了。而且三角形是有无数个的,你是永远也不能把所有的三角形全部证明一遍的。所以我们最好是找到一种通用的方法,来解决这个问题。
我这里有个巧妙的法子,你可以先来看看这个:

你看出他的特别之处了吗?反正我没有。因为我还没有给条件。
这是两条平行线,他能够帮助我们巧妙的解决三角形内角和的问题。什么?毫无头绪?那让我稍微帮助你一下,再在这上面写点什么吧:

有点思路了吗?也许这仍然很困难,不过想想我们的目的是什么?你一定还记得是跟三角形有关的吧?所以无论如何,首先要先做出个三角形来再说。
事实上,无论你做出哪个三角形,都能按照我们上述的证明方法来证明该三角形的内角和为180度。不过我更希望你能这样想,从上面一条直线的左边无限远处有一个点A,这个点A与下面的线段BC所形成的三角形ABC显然能够被证明内角和是180度。
接下来比较烧脑,你要想象这个点A在缓慢的向右移动,而与此同时在每个位置所形成的三角形都可以被认为是一个新的三角形ABC,并且新形成的这个三角形也可以被证明内角和为180度。
点A会继续向右移动,能移动到多远呢?无限远!意思是,想要多远就能有多远,只要你能想得到。所以,我们就可以认为在该直线上任意选取一点A,与线段BC所形成的三角形内角和都为180度。
也许你想说,在无限远处外面呢?其实,通过刚才我们的证明你应该已经发现了,只要点A还在这条直线上,那么就一定有三角形的内角和为180度,无论他是否像我们刚才说的那样,是在被“证明了”的范围内。
但我还是觉得你应当见识到这一想法,那就是对于无限远处,他可以被认为是直线的最左端和最右端。当然,在事实上直线是没有端点的,无论是左端点,还是右端点。但我们已经提到了无限,所以我们可以这样认为。
事实上,你也找不到比无限远处更远的了。如果你能举出一个例子,那么无限远处,当然要比你举的这个例子的数字要大。
所以,没有比无限远处更远的位置了,因此我们才能说认为无限远处是直线的端点。
并由此,我们可以认为我们刚才所做的行为已经证明了:该直线上所有的三角形,内角和都为180度。
当然,你并不一定要这样来想,之前的方法也是完全可以解决这样一个问题的。不过,见识多一点总归是没有坏处的,对吧?我们以后会提到跟他相似的东西的。
好了,到现在为止,我们总算是证明了三角形的内角和为180度。
不过,要是再严谨的话,你怎么知道直线外的另一条平行直线上,三角形的内角和也为180度呢?
好了,我们不继续说了,因为你仍然可以通过刚才的方法解决这个问题。
不过我这里有另一种方法。既然你已经证明了,在这条直线上所有的三角形内角和都为180度,那么你做一条线段AC的平行线,该平行线一定会与其余所有要证明的其余的与BC平行的平行线有交点,且与原直线BC有交点。而根据我们之前有的:两只线平行同位角相等,你可以很轻易的证明新形成的三角形内角和与原来的三角形内角和是相等的。因此,你就能够证明所有的三角形都与原直线上的三角形内角和相等,也就是说,无论是怎样的三角形,都一定有一种办法与原来的三角形相对应,那么也就具有相同的内角和了。而我们又知道原来的三角形内角和为180度,那么新的三角形的内角和也一定为180度。
到这里,我们算是完美的解决了这个问题,可以确切的说,所有的三角形内角和都为180度。
不过我还想再给你开开眼界,在某些情况下,三角形的内角和可以不为180度,事实上在这种情况下,甚至平行线会相交。但这些都是一些特殊的几何学,简单来讲,那是在曲面所运用的知识。
由于我们通常并不需要解决在曲面内的情况,因此我们之前所讲的一切都是在一个完美的平面内所能够得到的结论。
拓展就到这里。
不过我需要向你说明的是,刚才我们所说的三角形对应的关系,其实有另一个词,那够很好的代替他,那就是相似。
是不是听起来就感觉非常的恰当?
接下来我们将首先尝试解决勾股定理,这能帮助我们更好的解决在直角三角形中的相似问题。














