我们上一张说完了直角三角形的面积的公式:a×b÷2,也可以表示为:a×b/2,这两个都是没有问题的。实际上,第二种就相当于是把第一个的除号以一种分数的形式体现出来的,并没有本质的区别。
以上算是对上一章的面积的一个小小的回顾。
总之,你现在已经学会了在这幅图中直角三角形的面积如何求。
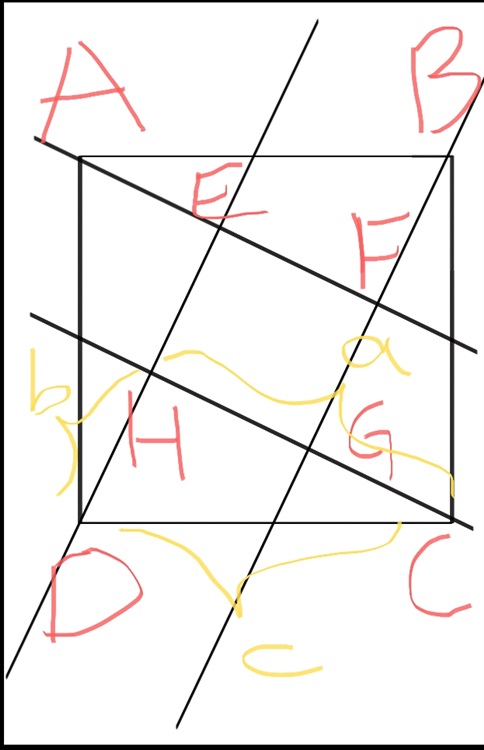
那么还记得我们说面积是为了什么来着吗?
我们说到这整个图形的面积可以认为是一个大正方形的面积,或者是四个小的直角三角形的面积,加上中间的一个小正方形的面积之和。
我们刚刚学的面积公式,就是为了用第二种方法来表示这整个图形的面积。
现在你知道每个直角三角形的面积都是a×b/2。由于一共有四个,并且你已经证明了他们全等,所以用四乘上这个式子就是这四的直角三角形的总面积了。
那么结果就是(axb/2)×4=2ab
请注意,在上面,我把一个直角三角形的面积的表达式用括号括起来了。这是因为,如果不加这个括号的话,这个式子就有歧义了。因为不加括号的话你就不知道这个式子表示的意思是:4乘以这整个分数,还是仅仅乘以分母?这区别可就大了。一个是变为原来的四倍,另一个是变为原来的1/4。
所以,为了防止这种情况,我特意加上了这个括号,这样就不会再有歧义了。
好了,那么我们到现在就只有所有直角三角形的面积之和为2ab,而我们又证明了中间的是一个正方形,所以我们只需要求出他的边长就知道面积了。
你可以直观的,看出它的边长等于三角形段一个直角边减去另一个三角形的较短的直角边。由于你证明了所有的直角三角形全等,所以另一个直角三角形的短边也就相当于这个直角三角形的短边。
(上文中,我说的“这个”就是图上标了边长为abc的这个三角形,而“另一个”就是右边的那一个)
也就是说,中间这个小正方形的边长等于下面这个三角形的长的直角边减去短的直角边,也就是a-b。
有个事情想告诉你,如果用一个用加法或者减法表达的式子来表示的结果后面有单位的话,一般是要加上括号的。
当然,其实不加应该也不会出现歧义,甚至于有时要求不加。
由于我的目的是想让你学会一些知识,但是对于这个问题,基本上属于一种习惯了,这并没有什么值得讨论的,就相当于是一个定义而已,如果所有人都认为应该加,那么就应该加。如果所有人都认为不应该加,那么就不应该加。
所以,我不会在这方面向你过多解释,如果你不是学生的话,你也不需要搞清楚这个问题,如果你是学生的话,那么我建议你问问你的老师,你的老师一定会比我更清楚适合你现在的正确答案。因为据我所知,在不同的学习阶段,对此有不同的要求。
所以我们就不要在这个问题上钻牛角尖了。
总之,我们知道了边长,那么面积就应该是他的平方,用大白话说,就是用它乘他自己。
(突然想起自己连指数都没说,就在前面用那样的形式来表示勾股定理!我们以后会再次提到相关知识的)
所以正中间那个小正方形的面积应该表示为(a-b)²,也就是(a-b)x(a-b)。前面那个式子右上角的二就代表他下面的这个括号里的东西乘他自己两次。前面表示勾股定理的式子跟这里同理。
根据我们之前学过的(突然发现我之前连多项式相乘都没说过!)乘法的知识,我知道我们没讲过类似的,所以我们仍然将从最基本的知识说起。
我们采用类比的思想,2×3,就是两个三相加。所以(a-b)x(a-b),就相当于是a-b个a-b相加。
我知道这可能有点难以理解,让我们好好捋一缕。
所以,a-b个a-b相加,就相当于是a个a-b相加的和,减去b个a-b相加的和。
现在再进一步捋一下,这其中a个a减b相加的和,就像上面一样,相当于是a个a相加的和,减去a个b相加的和。用乘法表示的话,就是a×a减去a×b。
而b个a-b相加的和,跟上面的思路基本相同,就是改个字母而已。(所以你应该不介意我直接复制粘贴,然后改个字母吧?)相当于是b个a相加的和,减去b个b相加的和。用乘法表示的话,就是b×a减去b×b。
还记得我们前面说过的吗?a-b个a-b相加,就相当于是a个a-b相加的和,减去b个a-b相加的和,所以,我们要用a×a-a×b-(b×a-b×b),化简一下,就是a×a-a×b-b×a+b×b(这一步化简可是加减法了,你应该没问题吧?),再次化解一下,比如使用我们刚才提到的,在右上角写二的形式,以及把-a×b-b×a用(-a×b)x2的形式来表达,我们最终可以得到,结果为a²-2ab+b²。
所以,(a-b)x(a-b)就等于a²-2ab+b²。也就是说,中间那个小正方形的面积就等于a²-2ab+b²。
而我们刚刚又证明了,剩下的四个小三角形的面积之和为2ab,所以让他们相加(这种加减法就没问题了吧?),显然,结果就是a²+b²。
而我们又知道这整个图形的面积还可以表示为c²。这整个图形的面积,难道能是两个值吗?不可能。所以唯一的答案是,这两个数相等,也就是说a²+b²=c²。
又一次,我们整理思路整理了两章。我很有感触啊。但是这些感触还是在有感而发之作里说吧。
现在说回正题,我们刚刚在多项式之间的乘法这一部分花费了大量的时间,因此下一章我们将从这个基本的例子出发,归纳并总结出多项式之间乘法的运算法则,那么顺带的,我们就将提到多项式之间乘法的逆运算,也就是除法的一些性质。














