接下来让我们先放弃正方形,转而研究三角形全等的相关知识,这将让我们在面对正方形在内的,众多能够在内部以分割的形式形成三角形的各类图形时,能够更好地研究它们的性质。
事实上,这已经不是我们第一次接触三角形全等了。
在我们证明勾股定理的时候,我们已经说过的一种能够证明三角形全等的条件了。
不过在这里我要再次重申,我们研究的所有全等的条件都是要尽可能的以最少的条件来得出全等的结论,而根据前人的经验,当然你也可以自己尝试一下,在三角形的三条边和三个角这六个条件中,如果只有两个的话,是不可能证明出两个三角形全等的。
至少得有三个条件,才有可能证明两个三角形全等。
四个当然更能,但由于找四个条件,显然并不能是最简的方法,显得麻烦,所以我们一般不讨论四个条件。五个条件和六个条件也同理。
事实上,找六个条件的话,这基本上算是个定义了,那还证什么?
考虑现实,这可能就会让你更好理解,因为在现实中你去测量的话,是一定会有误差的,而你测的数据越多,你的误差就越大,所以就越不精准。
而如果你能用较少的条件的话,由于你测量的越少,所以一般情况下你得到的结果就会更加的精准。
所以我们在研究三角形全等时,一般只考虑如何以最少的条件去证明两个三角形全等。
现在又回到我刚才说过的,因为两个条件不能证明三角形全等,最少也要三个,所以我们一般只研究哪三个条件能够证明三角形全等。
接下来我拓展一个小小的东西,真的很简单,那就是,另外一种证明三角形全等的方法。
那就是,把一个三角形撕下来,然后放在另一个三角形上,如果他们恰好能完全重合,那么就证明这两个三角形全等。
当然,你现在的我们来看这个方法可能过于复杂,而且操作过程比较麻烦,所以我们一般不这样做。但我告诉你,这样一种方法的原因,就是让你更加深刻的理解,三角形全等的含义,就是一模一样。如果他们两个都能完全重合的话,那肯定一模一样。
这种方法在我们学习之前你也许可以用一用,但在我们学习全等知识后还是不要用了。
尤其是有时候你也用不了啊。
比如说在一个国宝上面,我们就假设它的价值几十个亿吧。你想判断一下这个国宝上面的两个三角形是不是一模一样的,难道你要直接把这个国宝上次三角形切下来比较一下吗?
反正我可不敢切。
好了,废话扯了这么多,我们回到正题。
我们之前提到过了一种全等的证明方法,那就是只要有两个角相等,然后这两个角中间的边相等,那么我们就可以说这两个三角形全等了。
请注意,我在这里表示的不是特别规范,严格的来说,应该说是两个三角形的对应的边或者角相等,也就是说一组角或边对应相等。因为我说的是在两个三角形中,这两个对应的角或者是边具有相等的关系。但为了方便,我就简单说角相等和边相等了,你理解就行。
这种两组角和一组边对应相等的方法,尤其是这种两角夹一边,我们一般称呼他为ASA。这里A表示的是角,S表示的是边长,所以你应该很明显的看出来这个符号表示的是什么意思吧?就是两个角及其夹边相等。
我直接给你列出其他所有证明三角形全等的方法吧!
ASA,AAS,SAS,SSS。
非常的浅显易懂,对吧?
第一个是我们刚才说过的,两角及其夹边相等。
第二个就是任意两个角和一个非夹边的边相等。注意,只要不是夹边就行。
接下来我会为你解释,第二个方法能成立的原因。如果有任意两个角相等的话,根据三角形内角和为180度,你就能够证明这两个三角形的三个角完全相等,而又有一个边相等,所以他现在就可以被转化为第一种情况,所以第二种也成立。
第三种,就是两个边相等,而这两个边所形成的角也相等。
接下来我就为你解释,这第三种为什么也能证明全等。当角都被确定后,由于要形成一个三角形,所以相当于是三角形的一个点被确定了,由于这两个边的长度一样,所以另外两个点也就是确定了的。
而如果另外两个点被确定了,那么连接这两个点所画出的线段也一定是确定了的。
或许你要说,由于不确定用哪一条确定的边作为那个确定的角的一边,也就是说那个确定了的脚上的确定的两个边可以互换位置,所以不能确定另外两点是一样的。
实际上,这不过是左右倒个位置而已,就像你照镜子,你挥动左手镜子里的你却挥动右手,但你们绝对是一样的。
第四种,就是三个边对应相等。
关于这个的证明,我觉得用一张图来解释比较好。
比如我们先做出一个边,然后分别以两条确定了的另外两条边的边长做为半径画两个圆,如图:
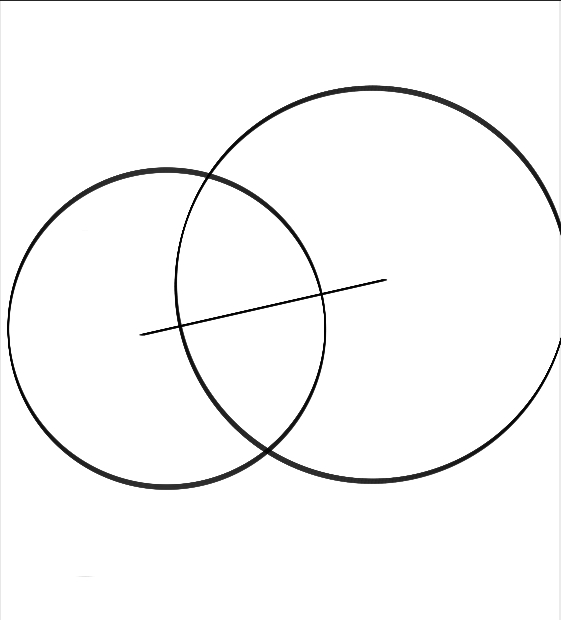
你注意到这两个圆只有两个交点,也就是说,如果你确定了三边的长度,你只能画出两个三角形。而实际上,这两个三角形也像我们刚才说的一种镜像的关系一样,他们其实是完全一样的,只是一个在上面,一个在下面而已。
好了,这就是证明三角形全等的四种方法。不过我还要说明的一点是,如果是在考试中的话,你可能还需要有一定的格式,并且格式随着不同学段有着不同的要求。
初中应当是最严格的,因为这个时候题都很简单,为了刻意的给你增加一些麻烦,所以可能会对格式有一些比较严格的要求。
而如果在高中的话,由于题比较难,这些复杂的格式耗费了,我们大量的时间,所以我们一般不再需要像初中那样严格的格式。
如果你对格式方面还有疑问的话,我建议你最好问问你的老师。不过即使你不会格式也无伤大雅,因为比起记住格式的话,理解显然更加重要。谁知道以后会不会有一种新的格式来代替他呢?毕竟真理不会改变,但掌握真理的人,可是会改变的。














