我说过我要带你从勾股定理中探寻出一些无理数。
现在就让我们开始吧!
其实很简单,首先我们需要一个三角形,一个直角三角形,一个两直角边都为一的三角形。
他看起来应该是这样的。
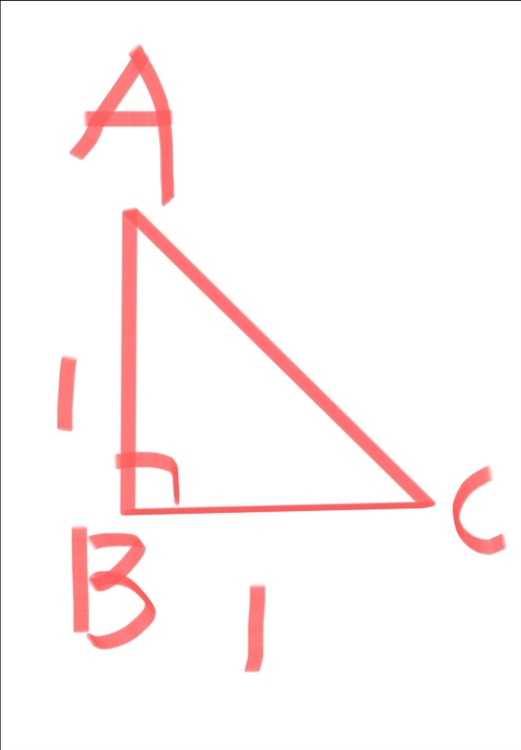
我们之前学到过勾股定理,而现在我们又知道这两个直角边都为一。
因此,你可以轻易地求出,另外一条边的平方,也就是斜边的平方。
它应该等于,一的平方加上一的平方,等于二。
不过现在问题来了,哪一个数乘上他自己,也就是平方后等于二呢?
你也许会尝试着从1.1开始尝试,然后是1.2,1.3, 他们都不能平方后得到2。
如果好的话,你会发现1.4就已经很接近,并且1.5就大了,所以你觉得这个值一定在1.4和1.5之间。
如果不好的话,你可能会直接暴躁到想直接把手机摔了。
为什么不试试用计算机呢?
如果你去尝试的话,你也许会发现你无论怎样都找不到某个确切的值,每次尝试你都会发现他在某两个数之间,于是你不断的去在这两个数之间逼近,这样你的最终结果越来越接近于二,但是你快要崩溃了,因为你发现你永远都到不了2。
事实上,这个数是没有最后一位的。换句话说,这个平方后等于二的数字,是没有办法被,用小数的形式给完整的表示出来的。
你永远不可能把这个值写完,它后面连着一大串数字。
不过我说了这么多,无非是站在一个已经知道的视角来解释这些已有的东西。
就算到了现在,可能也会有人坚持认为,只是小数点后的位数找的还比较少而已。总会有一个能写出来的数它的平方等于二。
所以,接下来我就将用一个巧妙的小方法来给你解决这个问题,向你证明他与我们以前见过的数是不一样的,他会是一个拥有无限多个小数点后的位数的数。
不过在我解答之前,还是让我先简单的说明一下,我所使用的方法吧。毕竟你看我解释一遍,没什么用,你学会自己去解释,也许是一个更有用的事。
我将要用到的是反证法。简单来说,结合这个具体的例子,我想要证明的是这个数是一个与我们之前见过的数不一样的,没有最后一位的数。
(你应该能明白我所表达的意思吧?他指的是拥有无限多个小数点后的位数。我们姑且可以先把它简称为无限小数)(为了你的阅读方便,我将这一部分单独成段,你应当从上一段看完后直接跳到下一段看)
那么反过来,我只要证明这个数不是一个有最后一位的数,那么不就能证明这个数是一个没有最后一位的数了吗?
听起来有些绕,总而言之,我会向你解释,为什么这个数没有最后一位。
首先,根据我们之前的经验,无论这是个什么样的数字,只要他有最后一位的话,那么这最后一位肯定是在一到九之间的这几个数中。
在这里可没有零了。因为零相当于没有,这可不是在整数中,这是在小说里。0.1和0.10有什么区别呢?换句话说,就这两个数向你表示的信息来说,它们是相等的。所以就算真的有一个零,你也应当无视他。毕竟,在各种运算中,这最后一个零是没有什么影响的。
所以我们不会出现有0.10这种表示的方法。当然,不是数学相关的方面的话,我可就不管了。
回到正题,所以你现在应该能理解了一个有限的小数的最后一位必定在一到九内。事实上,这显而易见,其实我刚才没有说明,你很轻松就能想到这一点。
那么接下来我将继续。
首先根据我们的定义,我们要证明的这个数平方后等于二,所以它们相乘后最后一位,(假设有最后一位)之间的运算,一定是1×1,2×2,3×3这种自己乘自己的。
同时,由于我说过他们是最后一位相乘,所以他们最后出来的结果一定就是最终结果的最后一位。
但我们知道我们要求的最终结果必须是二,也就是说结果的最后一位就是二,所以这就要求我们所寻找的这个数的最后一位相乘也必须得是二。
很好,问题到现在就很简单了。
在一到九这九个数内,有哪个是用它乘以它本身等于二呢?
一一得一,二二得四,三三得九…,剩下的我就不说了,总之,你现在应该意识到的是没有任何一个数乘他自己等于二。
所以也就是说,不可能有这个数存在,因为无论他的最后一位是多少都无法完成平方后等于二的要求。
但是,我们还有一个想法。
这个数可能是一个无限的小数。简而言之,就是说这个小说不是是一个有无限多个小数位的数。听上去很像一种暴力的方式,像是一种耍赖,因为最后一位不可能,所以干脆就直接让他没有最后一位?
原来是用这种方式来解决的吗?
你先别急,你忘记了我们之前也遇到过一些类似的数吗?
比如1/3。
他也无法用小数的形式来完全表示出来,但是它确实存在,而且看上去很好理解。
事实上,这个平方后等于二的数,也跟这个1/3一样,是一个有无限个小数位数的数。
不过他们之间也有一些不同。
比如1/3,它的小数部分就是无穷多个三。
但是这个平方后等于二的数呢?他没有规律。
换句话说,这种用分数表示出来的数,它的小数部分都是有一定的周期性。
就是说,某几个数每隔一段时间就从头到尾的来一遍。
比方说,可能有某个小数为0.114514114514114514,就这么不断的114514下去。我说的是不断的重复下去。
而这个平方后等于二的数,他就完全没有这种事情发生。当然关于这方面的证明,我们还是要等到以后。
所以现在,你应当能接受,确实存在一个数,它的平方后等于2。
到现在了,你觉得这么形容是不是有点长了?
为了简单,我们将此表示为√2。读作“根号二”。
好了,那么关于这种无理数的引入,我们到这里,就算是结束了。
接下来我将向你介绍一些关于实数分数这种有理数的证明方式,就是说怎样判断一个数是有理数,这将使我们更好地了解到无理数与有理数所不同的性质。
同时,知道判断有理数的方式后,我也能以一种更加严谨的方式来向你证明这个根号二是一个无理数。














