用综合评价与决策方法解决最佳拍档问题
摘要
最佳拍档的选择至关重要,在大学生数模竞技比赛中作用更为突出,正所谓“逸一时误一世”,科学的拍档选择不可或缺,所以本文运用综合评价与决策的方法研究最佳拍档问题。
针对问题一:数学建模重要能力指标分析。本文采用辩证分析的方法,全面深刻地分析了除了基本数学素养以外的其他数学建模竞赛素养要求,形成了较为全方位的能力要求分析,特别指出了如下几项能力素质要求:学习能力、建模能力、代码能力、写作能力、协作能力。
针对问题二:寻找队友的重要指标分析。本文在Matlab上化繁为简地优化运用了层次分析法(AHP),对各个重要指标进行权重附加。首先构建了层次结构图,理清了目标层、准则层、措施层,再构建准则层的判断矩阵A,进行列向量归一化得到矩阵B,再按行求和得到若干矩阵。再经过一系列检验,成功通过了一致性检验,最后对其重要性进行了排序,找出了找寻队友所需的几项最重要的指标:建模能力、写作能力、代码能力。
针对问题三:三人队伍的合理性以及未来的职能分配。本文运用了综合评价与决策的方法,灵活地在SPSS中进行数据可视化处理,将附件二中的a,b,c三位学生的各个能力用三个柱状图和一个饼状图充分展现——建模能力:b>c>a;写作能力:a>c>b;代码能力:c>b>a。再进行合理的决策,肯定了三人队伍组建的合理性以及发现了其互补性。最终规划三人未来负责的职责方向:b适合做建模手,a未来可以成为论文手,c可以做编程手。
最后,将各个问题联系起来,形成了一个综合的评价与决策方案,可以让我们更好地解决最佳好拍档的问题。
本文所建成的综合评价与决策的方法能与实践充分结合,知行合一,具有极大的推广意义,是科学的指南。
关键词:层次分析法(AHP) 综合评价与决策方法 数据可视化 模型优化
一、问题重述
古人言之,一个巴掌拍不响,高校中的学生数学模型竞技比赛也如此:不是一个人的王者,而是团队的荣耀。如何组建一个数学模型竞技大赛的团队,寻找最佳好拍档就成了我们不得不面对的实际问题。
尝试对新人同学组建数模竞技比赛团队的相关情景,对其进行数学建模分析,以研究以下问题:
(1)数学建模竞技比赛是综合能力的考验,对参赛选手的数学能力和素质有着一定要求,对选手的其他素养要求也充满了多样性和交叉性。请简要叙述数学模型竞技比赛对选手的其他素养的要求并给予一定分析。
(2)团队需要队友的有机组合,挑选队友意义重大。通过已给的附件1中的有效信息,综合考量各种因素,请找出其中极为重要的指标。
(3)一个数学模型建模团队一般有“三剑客”:建模者、论文客、编程家。附件2中给出三人小队中各位成员的能力指标,试分析他们组队是否符合竞赛能力分配要求以及他们未来的职责方向。
二、问题分析
2.1问题一的分析
对于其他素养的要求其实不难得知,只需综合考量,具体问题具体分析,运用全面辩证的方法即可得知。
2.2问题二的分析
要分析寻找队友的重要指标,首先应该根据问题一中考量得出的数模竞技比赛所需的各种素养要求,综合分析,然后通过评价类模型给它们的权重可视化,筛选出几项最为重要的指标要求。
2.3问题三的分析
要研究他们的三人数学模型竞技比赛的队伍的组建的合理性,首先应根据问题二中各指标的重要性去分析研究与契合,再通过附件二中的他们三人所体现的各种能力,本文通过综合评价与决策的方法进行合理性甄别以及他们未来职能的分配的比对研究。
三、模型假设
1.假设他们都热爱数学建模,没有好逸恶劳的想法,能各司其职。
2.排除队员之间的社交关系干扰。
3.假设排除性别因素差别,队员无男女之分。
四、符号说明
表1符号说明
符号
定义
单位
A
矩阵A
/
C
矩阵C
/
五、模型的建立与求解
5.1问题一:数学建模重要能力指标分析
对于数学建模竞技,除了最基本的数学素养,还应当具有其他综合能力。譬如:学习能力、建模能力、代码能力、论文写作能力、协作能力。
这些能力指标都十分重要,学习能力要求参赛者对于新知识、新模型的输入以及输出有效率、有持久力;建模能力需要建模者熟悉掌握各大建模软件,善于分析一个问题所对应的数学模型解决方案;代码能力要求参赛者熟练掌握代码的运算和可视化输出的过程;写作能力需要文笔和排版的功底,关系到竞赛成果的最终体现和评分;协作能力则要求团队配合紧密、能力互补。
5.2问题二:寻找队友的重要指标分析
5.2.1模型一的建立——层次分析法(AHP)
寻找队友的指标有很多,但也有最为重要的几项。根据附件一并综合考虑个人的能力、队友所需、竞技比赛所需等,建立以下层次模型:
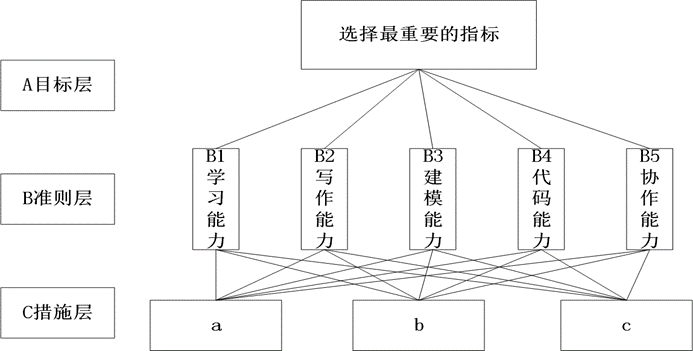
图1层次结构模型
5.2.2模型一的求解
准则层的判断矩阵A如下
图2准则层的判断矩阵A
按行求和得到矩阵C
图片3矩阵C
由此可以得知,最重要的指标是建模能力、写作能力、代码能力。
5.2问题三:三人队伍的合理性以及未来的职能分配
5.2.1模型二的建立——综合评价与决策
由表1可以得知三位学生的各方面能力体现,包括建模能力、写作能力、代码能力、协作能力、学习能力。
表1附件二
建模能力对应:建模能力;写作能力对应:写作能力;代码能力对应:代码能力;学习能力对应:高考数学、高考总分、平时成绩、期末成绩、每日平均学习时间;协作能力对应:班干与否、二课分。
由模型一可以得知,最重要的指标是建模能力、写作能力、代码能力。
根据附件2,并通过SPSS进行可视化处理,形成以下图表:
图4学生建模能力对比柱状图
图5学生写作能力对比柱状图
图6学生代码能力对比
5.2.2模型二的求解
图7学生能力饼图
根据综合评价与分析,他们这三人队伍具有一定的合理性和互补性,能很好地发挥各自优势。b适合做建模手,a未来可以成为论文手,c可以做编程手。
六、模型的评价与推广
6.1模型的优点
1)模型简单易懂,易于分析。
2)代码易于操作。
3)输出结果直观化、可视化、高效化。
6.2模型的不足
1)列向量归一化所需内存较多,对代码运算的电脑配置有一定要求。
2)对于完全的数模新手来说,难度巨大。
3)主观性较强。
6.3模型的推广
可用于人力资源管理实践中的绩效管理和员工考核,同时进行员工的分组与合作。
七、参考文献
[1]曹帅,陈国豪,陈应妮,刘文杰,刘宇苗等.学生数学建模协会培训教材[M]四川农业大学,2022














