终于还是来到了这个环节!小玖来给大家讲一些高中的不等式方法了!那么废话不多说,我们开始正题!
我们都知道,高中有一串基本不等式,而这基本不等式是足够解决正规考试的所有有关不等式的题目的,但是涉及到什么“乘1法”啊,“齐次化”啊……总之,如果遇上了一些比较难的题目,用常规思路是很难解决的!所以先给大家讲两个对我们做题很有帮助的两个不等式:权方和不等式与柯西不等式。
请看例题:
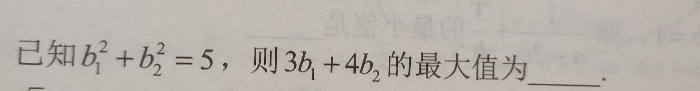
这么猛的一看下去,似乎有点让人一头雾水啊?题目给出了一个平方和的条件的式子,让求最大值……
不确定,赶紧看一眼我们的不等式链:
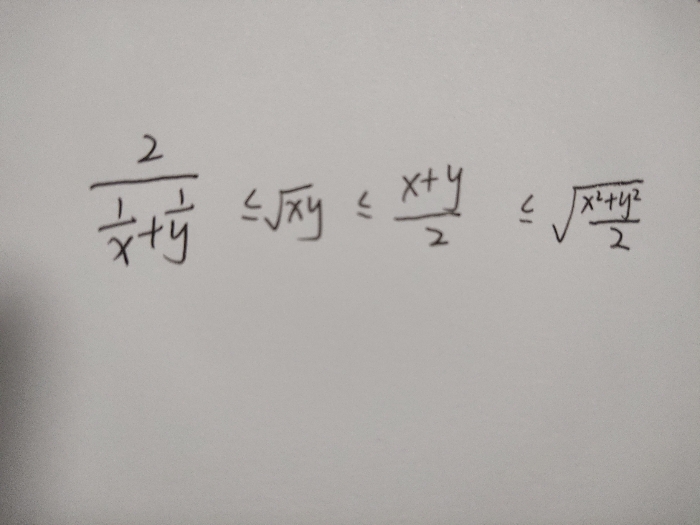
好吧……似乎越看越迷糊,这怎么看也不是我平常用的那些方法吧?于是乎我们这里就引进一个新的不等式:柯西不等式!

诶,仔细观察,这个柯西不等式,是不是左边就是一个平方和的形式?右边是和的平方。
冥冥之中似乎有些什么联系?
题目求两数和的最大值,所以说这两个数应该是小于或者等于某个最大值,这不刚好和柯西不等式大概样子对上了吗?
那我们接下来就该想的是,如何往柯西不等式的方向去配凑!
我们看到b1和b2前面有个系数,那么我们就把条件乘3²➕4²,得到了这么个东西

诶,在对比一下上面给出的二维形式柯西不等式,这3²➕4²不就是x1²➕x2²嘛?3b1➕4b2不就是x1x2➕y1y2嘛?
所以我们得到了
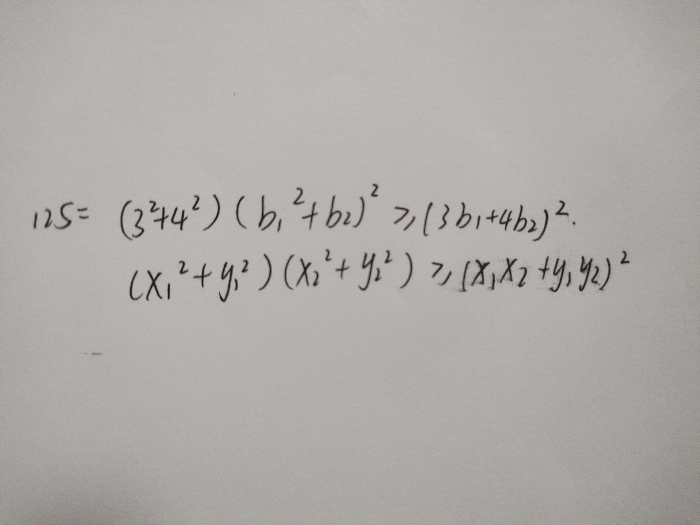
上面是我们配凑的式子,下面是原柯西不等式二维形式,所以这么一上下对比,你就发现,这可不就是把字母换了一下嘛!
因此我们很容易得出来,题目要求的最大值为5√5,当且仅当4b1=3b2时成立
好,那么我们上面提到了柯西不等式。那么假设我现在已经是一个了解柯西不等式的人了,那我该在什么情况下联想到柯西不等式呢?注意我上面说过的一句话:“条件中有平方和结构”
这句话就是我们联想到柯西不等式的初步依据,看下面这道题:(注意是初步依据)
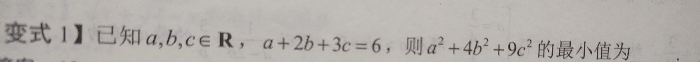
这道题目呢是求最值的式子中有个平方和结构,而且恰好是求最小值,那我们就该联想到三维形式柯西不等式了吧?于是解题过程就是:

很简便的过程吧?不过呢很多时候,没有平方和这个结构的题目大有很多,但是也可以使用柯西不等式快速求解,所以呢,能不能用好柯西不等式,就在于你是否对这两个二维和三维形式够熟悉。下面放一到练习给大家做做看:
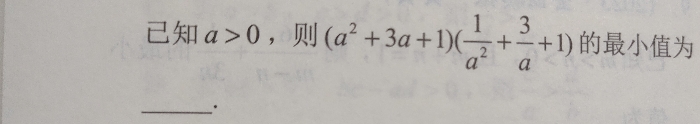
不过这道题用常规思路也是可以的,但是既然了解了柯西不等式,就尝试用用它吧。
第二个,权方和不等式
这个讲起来就简单多了,我们先来看看式子
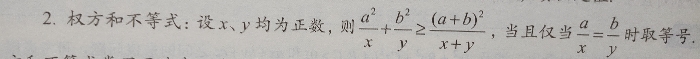
它有个很明显的特点:左边两个式子的分母和成为了右边式子的分母了!所以如果你发现左边两个式子分母和为定值的话,就可以尝试一下权方和不等式了!例如这样:

把两个式子的分子变成3²与4²,再套到权方和不等式里面去,是不是很容易就得出来答案是49呢?
权方和不等式是一个简单,实用的不等式,唯一运用起来的阻碍就是你需要往这个方向去配凑原不等式,下面放两道练习题

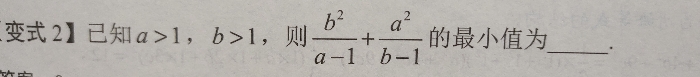
好,最后一个,三角换元法。
不知道你还记不记得我前面有一道题目用了三角换元法解决呢?
三角换元法,涉及平方和或者平方差的求最值问题,就可以考虑三角换元。

诶,你仔细看看,这个换元的第一个平方和条件,怎么是个圆的解析式呢?这就对了,这种换元方法在学习圆的时候,也是经常用到的。
那我们看题目吧
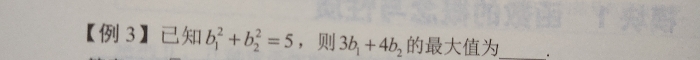

用上了一点三角函数的知识,不然怎么叫三角换元嘛!不过总的来说还是不难的吧?那如果还是老样子,换成需要配凑的形式呢?

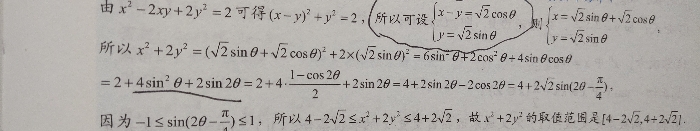
诶,这道题就有两个点得提一下子了。一个呢是第一步,把原条件配凑成一个圆的解析式,第二步,把x-y看成一个整体设成√2cosα,在把y移过去得到x设的形式,也不难对吧?
那么我在出道练习
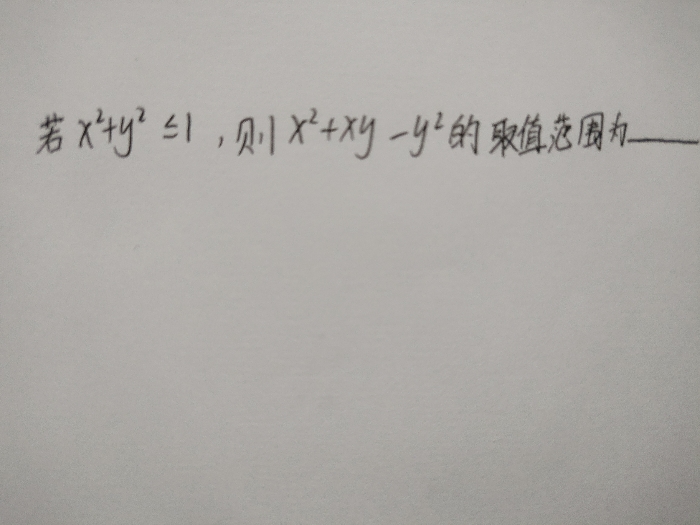
这道题目没有给出x²➕y²为一个定值这个条件,而是给了个范围。但是这并不妨碍我们用三角换元解决,既然不确定,那就用字母r代替,试着做做看吧?














