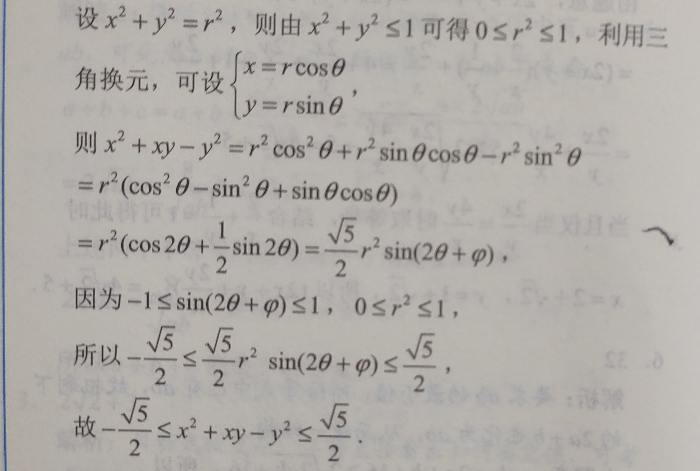呜啊,大家好啊,这一章是给出前面不等式进阶那一章节留下的练习的答案,虽然应该没人看吧,但还是给一下好了。
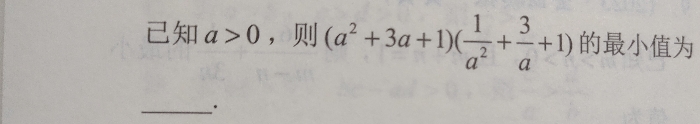
这个就是柯西不等式的练习题了吧,好我们先来观察一下这个式子。直接让求最小值,我们先来试一试常规思路吧。
把左边的每一项都正乘到右边去,即消去括号后,我们可以发现,整理一下得到的式子,就可以使用基本不等式,a➕b≥2√ab,得到我们需要的答案。
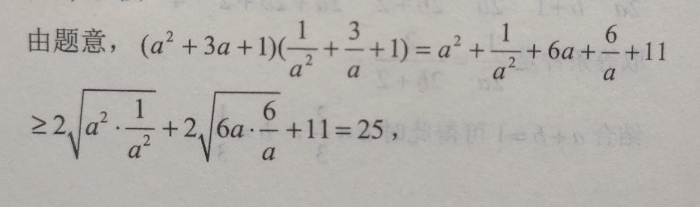
那我们再来试试用柯西不等式求解吧,要用柯西不等式,就得把他变成柯西不等式的形式,复习一下我们要用到的柯西不等式吧。
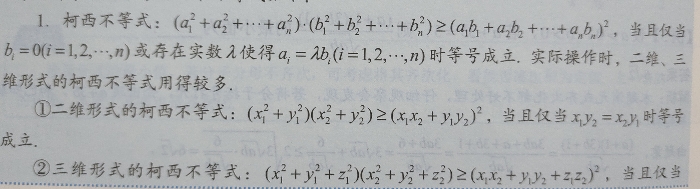
显然,柯西不等式都有个平方在里面,所以我们就把对应的数改为平方的结构,然后直接套用柯西不等式就可以得出答案啦
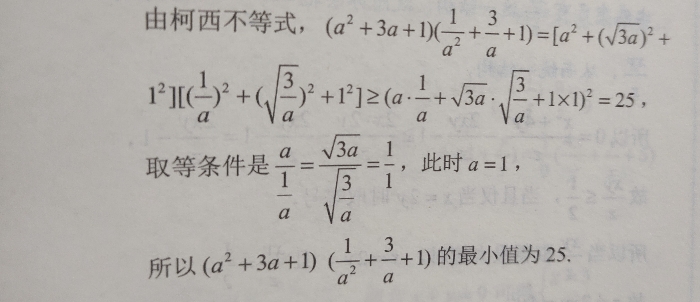
好嘞,那下面就来讲权方和不等式那两道练习题的答案喽。。。。。。。


第一道题还是很简单的,还记得我说过的嘛?权方和不等式最大的特点就是左边两个式子分母想加得到了右边的式子,此时刚好分母是个定值。这道题只需要稍作变形就可以达到这个要求了,就是把右边的b分之三上下两边同时乘3,然后用权方和不等式,最后带入已知的a➕b=1这个条件就可以啦,具体过程就是下面这个。
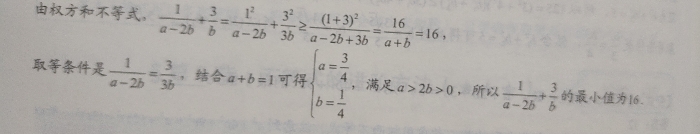
下面这道题稍微有点绕了个圈子,首先需要使用权方和不等式来创造条件,然后使用换元法搭配基本不等式求解,具体过程如下。
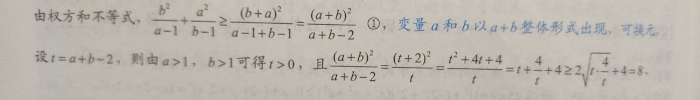
虽然无法使用权方和不等式求出答案,但是原式子的结构因为使用了权方和不等式而被我们化为了更优良的结构,所以帮助了解题。
最后这道题呢还有点来头,是2020年清华强基试题,看上去还挺吓人哈,其实只要掌握了三角换元的方法,是不难的。
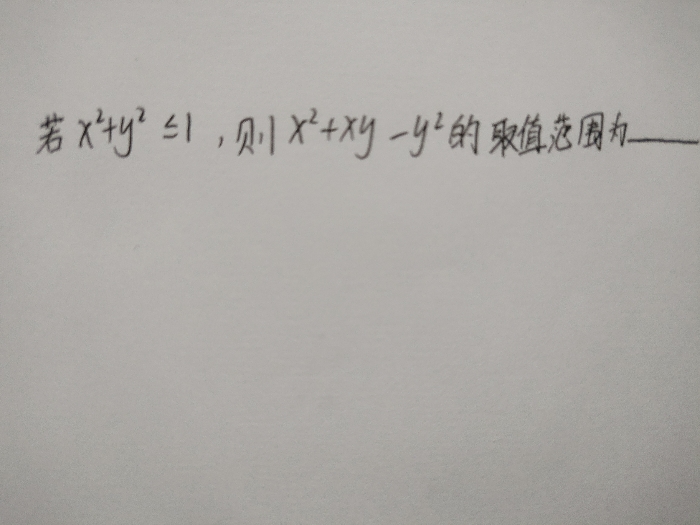
前面我提到过,这道题虽然给的x²➕y²条件是一个范围而非定值,但这不影响我们设值。既然不确定是什么值,那就干脆设为r吧。这样一来,x,y就都可以用r乘以三角函数的形式来表示了。
随后再把我们设好的值代入到要求解的式子中,结合三角函数的知识就能很轻松得出答案了啦~
下面是具体过程